Support vector domain description

发表于 2019-11-29

字数统计: 3 | 阅读时长 ≈ 1

One-class classification

Estimating the Support of a High-Dimensional Distribution

发表于 2019-11-21

字数统计: 273 | 阅读时长 ≈ 1

1、Generally, they can be characterized as estimating functions of the data, which reveal something interesting about the underlying distributions. For instance, kernel principal component analysis (PCA) can be characterized as computing functions that on the training data produce unit variance outputs while having minimum norm in feature space (Sch¨olkopf, Smola, & M ¨uller, 1999). Another kernel-based unsupervised learning technique, regularized principal manifolds (Smola, Mika, Sch¨olkopf, & Williamson, in press), com-putes functions that give a mapping onto a lower-dimensional manifold minimizing a regularized quantization error. Clustering algorithms are fur-ther examples of unsupervised learning techniques that can be kernelized (Sch¨olkopf, Smola, & M ¨uller, 1999).

核方法可被特征化为数据的估计函数，其揭示了数据潜在的分布。例如，给予核的PCA方法可被特征化为计算函数，该函数在训练集上产出特征空间中最小范数的单位方差输出。另一种基于核的无监督学习方法，regularized principal manifolds，这种计算函数通过最小化正则量化误差给出了原始数据到低维manifold的映射。聚类也是一种可被核化的无监督学习方法。

2、Section2 Previous Work

挖坑（知识有限，不能理解）

3、OCSVM

挖坑，SMO优化及改进

xgbt

发表于 2019-11-17

字数统计: 240 | 阅读时长 ≈ 1

GBDT梯度提升决策树

集成学习(Ensemble Learning)

集成学习是指构建合并多个学习器完成学习任务，又分为同质集成和异质集成。顾名思义，同质集成是指包含不同种类型的个体学习器，而异质集成则指代包含非同种的个体学习器。同质集成中的个体学习器亦称基学习器，而异质集成中的个体学习器亦称组件学习器。

我们所能听到的另一个词语，弱学习器，实际上是指我们上面提到的个体学习器。

目前集成学习方法可大致分为两类，一类是指个体学习器存在强相互依赖关系，串行化序列生成，另一类指同时生成的并行化方法，这两类分别是我们常说的Boosting和Bagging。

GBDT

XGBoost

GBDT与XGBoost解析与应用

代码实现

见github主页

hierarchical

发表于 2019-11-17

字数统计: 330 | 阅读时长 ≈ 1

层次聚类(hierarchical clustering)

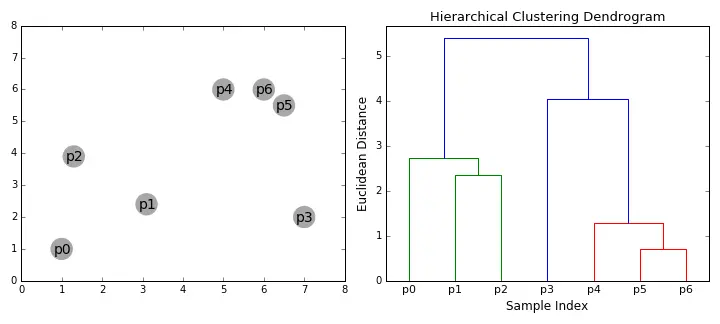
如图所示为层次聚类的基本算法流程：

初始化每个样本独自一个聚类。选取相似度最高的聚类合并，重复操作直到最小聚类数或相似度小于某阈值。

层次聚类类似于构建树的过程，因此在数据结构上可优先选取二叉树结构。

聚类相似度

各种距离计算不再赘述，而基于距离描述的相似度有以下几种方式：

Single Linkage $dist_{ij} = min\{\ enum(dist(m, n))\ \}, m \in C_i, n \in C_j$ 即取两聚类最近邻样本聚类作为两聚类的距离，受极端值影响较大，可能两聚类因为偶然离得比较近的两个点而被合并，导致最终得到的大聚类中的点分布较为松散
Complete Linkage $dist_{ij} = max\{\ enum(dist(m, n))\ \}, m \in C_i, n \in C_j$ 即取两聚类相距最远样本作为两聚类距离，与single linkage完全相反
Average Linkage $dist_{ij} = avg\{\ enum(dist(m, n))\ \}, m \in C_i, n \in C_j$ 即取两聚类之间两两样本平均距离，平均值计算总是被诟病受极端值影响较大，因此实际可采用中位数估计一定程度抵消该种弊病。

代码实现

见github主页

fcmeans

发表于 2019-11-14

字数统计: 450 | 阅读时长 ≈ 1

模糊C均值聚类(Fuzzy c-mean clustering)

模糊是指没有明确边界划分无法精确刻画的现象称为模糊。

对离散且有限的论域

$U = \{u_1, u_2, ..., u_n\}$

其模糊集可表示为

$F = \{\mu_F(u_1),\mu_F(u_1),...\mu_F(u_n)\}$

其中 $F$ 称为隶属度函数

介绍及引入

我们所谓的kmeans聚类，也就是c均值聚类，可以称之为硬C均值聚类。

给定样本集 $D = {x{1},x{2},…,x{m}}$ ，k均值聚类算法针对聚类所得簇划分 $C = {C{1},C{2},…,C{k}}$ 最小化平方误差
$min\ E = \sum_{i=1}^{k}\sum_{x \in C_{i}}\|x-\mu_{i}\|_{2}^{2}$
其中
$\mu_{i}=\frac{1}{|C_{i}|}\sum_{x \in C_{i}}x$

模糊概念的引入使得该聚类叫做软C均值聚类，允许每个样本属于一个或以上更多的聚类。可以设想，对于某个样本点，可构建到每个聚类的隶属度函数，设样本数为 $n$ ，聚类数为 $C$ ，则存在 $n*C$ 的隶属度矩阵，每个样本与聚类的硬距离乘对该聚类的隶属度总体求和保证最小，便是模糊C均值聚类所解决的问题。

原理

Fuzzy C-Means聚类所优化的目标函数如下：

$J_m = \sum_{i=1}^{N}\sum_{j=1}^{C}\mu_{ij}^{m}||x_i-c_j||^{2}, 0 \le m< \infty$

$m$ 为大于1的任意实数。（至于 $m$ 具体作用也没有深入考虑 $TODO…$

针对上述目标函数优化，采用启发式迭代。

$u_{ij}=\frac{1}{\sum_{k=1}^{C}(\frac{||x_i-c_j||}{||x_i-c_k||})^{\frac{2}{m-1}}}$ $C_j=\frac{\sum_{i=1}^{N}u_{ij}^{m}x_i}{\sum_{i=1}^{N}u_{ij}^{m}}$

迭代停止条件可取隶属度矩阵变化值小于某 $\xi$ 时停止。

代码实现

见github主页

2019.9.22 噩梦

发表于 2019-09-23

字数统计: 0 | 阅读时长 ≈ 1

tensorflow

发表于 2019-09-14

字数统计: 0 | 阅读时长 ≈ 1

ubuntu tips

发表于 2019-09-13

字数统计: 81 | 阅读时长 ≈ 1

创建应用程序快捷方式

快捷方式存放位置 /usr/share/applications/

sudo touch /usr/share/applications/empty.desktop
# empty 代指 应用程序名称
sudo vim /usr/share/applcations/empty.desktop

[Desktop Entry]
Type=Application
Name=empty
GenericName=emptytemp
Exec="/opt/empty.sh" #执行路径
Icon=/opt/empty.png  #icon路径
Comment=       #注释
Catagories=item1;item2;item3; #分类
Terminal=false  #是否打开终端

tensorflow tips

发表于 2019-09-12

字数统计: 887 | 阅读时长 ≈ 4

tf.InteractiveSession() 与 tf.Session()

sess = tf.InteractiveSession()
a = tf.constant(5.0)
b = tf.constant(6.0)
c = a * b
# We can just use 'c.eval' without passing 'sess'
print(c.eval())
sess.close()

而tf.Session()前必须构建好图，再创建session

# Build a graph
a = tf.constant(5.0)
b = tf.constant(6.0)
c = a * b
# Launch the graph in a Session
sess = tf.Session()
# Evaluate the tensor 'c'
print(sess.run(c))

tf.app.flags 与 python3 absl.flags

from absl import app

FLAGS = flags.FLAGS
flags.DEFINE_string('gpu', None, 'comma separated list of GPU to use')

def main(argv):
    print(FLAGS.gpu)

if __name__ == '__main__':
    app.run(main)

import tensorflow as tf

flags = tf.app.flags
FLAGS = flags.FLAGS
flags.DEFINE_float(‘learning_rate’, 0.01, ‘Initial learning rate.’)
flags.DEFINE_integer(‘max_steps’, 2000, ‘Number of steps to run trainer.’)
flags.DEFINE_string(‘train_dir’, ‘data’, ‘Directory to put the training data.’)
flags.DEFINE_boolean(‘fake_data’, False, ‘If true, uses fake data ‘
‘for unit testing.’)

def main():
    print(FLAGS.learning_rate)

if __name__ == '__main__':
    tf.app.run()

import argparse

parser = argparse.ArgumentParser(description="Demo")
parser.add_argument('-y', '--year', default='2019')
parser.add_argument('-m', '--month', default='Sep')
args = parser.parse_args()

def main():
    print(args)

if __name__ == '__main__':
    main()

tf.train.ExponentialMovingAverage

Some training algorithms, such as GradientDescent and Momentum often benefit from maintaining a moving average of variables during optimization. Using the moving averages for evaluations often improve results significantly.

tf.train.ExponentialMovingAverage.__init__(self, decay, num_updates=None, zero_debias=False, name="ExponentialMovingAverage"):

参数的移动平均验证效果优于最终训练的结果。

$shadow\_variable=decay*shadow\_variabe+(1-decay)*variable$ $decay = min(decay, \frac{1+steps}{10+steps})$

$shadow_variable$ 最初为参数的 $copy$ ，上次为指数衰减， $decay$ 为衰减速率，一般为 $0.9, 0.99$ 等接近 $1$ 的数。

一般来讲，decay越大模型越稳定，因为参数更新更慢，趋于稳定。

import tensorflow as tf

# 定义一个32位浮点数的变量，初始值位0.0
v1 = tf.Variable(dtype=tf.float32, initial_value=0.)
# 衰减率decay，初始值位0.99
decay = 0.99
# 定义num_updates，同样，初始值位0
num_updates = tf.Variable(0, trainable=False)
# 定义滑动平均模型的类，将衰减率decay和num_updates传入。
ema = tf.train.ExponentialMovingAverage(decay=decay, num_updates=num_updates)
# 定义更新变量列表
update_var_list = [v1]
# 使用滑动平均模型
ema_apply = ema.apply(update_var_list) # return an operation that updates the moving averages

with tf.Session() as sess:
   # 初始化全局变量
   sess.run(tf.global_variables_initializer())

   print(sess.run([v1, ema.average(v1)]))
   # shadow_variable = variable = 0.
   sess.run(tf.assign(v1, 5))
   sess.run(ema_apply)
   print(sess.run([v1, ema.average(v1)]))

可参考吴恩达 $deeeplearning.ai$ 指数加权平均。

tf.add_to_collection 与 tf.get_collection

import tensorflow as tf;  

v1 = tf.get_variable(name='v1', shape=[1], initializer=tf.constant_initializer(0))
tf.add_to_collection('loss', v1)
v2 = tf.get_variable(name='v2', shape=[1], initializer=tf.constant_initializer(2))
tf.add_to_collection('loss', v2)

with tf.Session() as sess:
	sess.run(tf.initialize_all_variables())

	print tf.get_collection('loss')
	print sess.run(tf.add_n(tf.get_collection('loss')))

例如在使用L2正则化，网路各层变量需计算tf.nn.l2_loss，将其加入loss列表，最后创建操作求和。

tf.control_dependencies

with g.control_dependencies([a, b, c]):
#’d’和’e’只会在’a’,’b’和’c’运行之后运行
  d = ...
  e = ...

tf.name_scope 与 tf.variable_scope

知乎 tensorflow.name_scope如何理解

总结
1.tf.variable_scope 与 tf.get_variable 必须搭配使（全局 scope 除外）
2.tf.Variable 可以单独使用，也可以搭配 tf.name_scope 使用，给变量分类命名，模块化
3.tf.Variable 与 tf.variable_scope 搭配使用不伦不类，不是设计者的初衷

当前环境作用域可通过 tf.get_variable_scope 获取。

tensorflow.contrib.slim API

import tensorflow as tf

input = ...
with tf.variable_scope('conv1') as scope:
    kernel = tf.get_variable(name='weight', shape=[3, 3, 64, 128], initializer=tf.truncated_normal_initializer(stddev=5e-2, dtype=tf.float32), dtype=tf.float32)
    conv = tf.nn.conv2d(input, kernel, [1, 1, 1, 1], padding='SAME')
    biases = tf.get_variable(name='biases', shape=[64], initializer=tf.constant_initializer(0.0), dtype=tf.float32)
    conv1 = tf.nn.relu(tf.nn.bias_add(conv, biases), name=scope.name)

# slim convolution 原型
convolution(inputs,
        num_outputs,
        kernel_size,
        stride=1,
        padding='SAME',
        data_format =None,
        rate = 1,
        activation_fn = nn.relu,
        normalizer_params=None,
        weights_initializer = initializers.xavier_initializer(),
        weights_regularizer = None,
        biases_initializer = init_ops.zeros_initializer(),
        biases_regularizer = None,
        reuse = None,
        variables_collections = None,
        outputs_collections = None,
        trainable = True,
        scope = None):

import tensorflow as tf
import tensorflow.contrib.slim as slim

input = ...
net = slim.conv2d(input, 128, [3, 3]. scope='conv')

slim简化更有利于复杂网络编程，slim更多内容请参考官方说明

Github tensorflow/contrib/slim说明

kmeans clustering

发表于 2019-09-11

字数统计: 732 | 阅读时长 ≈ 3

k-均值聚类（k-means clustering）

聚类试图将数据集中的样本划分为若干个通常是不相交的子集。

距离计算 $dist(\cdot,\cdot)$

对函数 $dist(\cdot,\cdot)$，若它是一个距离度量，则需满足：

非负性： $dist(x{i},x{j}) \geq 0$
同一性： $dist(x{i},x{j}) = 0$ 当且仅当 $x{i} = x{j}$
对称性： $dist(x{i},x{j}) = dist(x{j},x{i})$
直递性： $dist(x{i},x{j}) \leq dist(x{i},x{k}) + dist(x{k},x{j})$

给定样本 $x{i} = (x{i1},x{i2},…,x{in})$ 与 $x{j} = (x{j1},x{j2},…,x{jn})$ ，最常用的是“闵可夫斯基距离”（Minkowshki distance）

$dist_{mk}(x_{i},x_{j}) = (\sum_{u=1}^{n}|x_{iu}-x_{ju}|^{p})^{\frac{1}{p}}$

当 $p=2$ 即欧式距离（Euclidean distance）。

当 $p=1$ 即曼哈顿距离（Manhattan distance）。

上式仅适用于有序属性（ordinal attribute），针对属性定义域{飞机，轮船，火车}等则属于无序属性（non-ordinal attribute）。

对于无序属性可采用VDM（Value Difference Metric），令 $m{u,a}$ 表示在属性 $u$ 上取值为 $a$ 的样本数， $m{u,a,i}$ 表示在第 $i$ 个样本簇中在属性 $u$ 上的取值为 $a$ 的样本数， $k$ 为样本簇数，则属性 $u$ 上两个离散值 $a$ 与 $b$ 之间的VDM距离为

$VDM_{p}(a,b)=\sum_{i=1}^{k}|\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}|^{p}$

假设混合属性有 $n{c}$ 个有序属性、 $n-n{c}$ 个无序属性，则

$MinkovDM_{P}(x_{i},x_{j})=(\sum_{u=1}^{n_{c}}|x_{iu}-x_{ju}|^{p}+\sum_{u=n_{c}+1}^{n}VDM_{p}(x_{iu},x_{ju}))^{\frac{1}{p}}$

当样本中属性重要性不同时，可使用“加权距离”（weighted distance）。

$dist_{wmk}(x_{i},x_{j})=(w_{1} \cdot |x_{i1}-x_{j1}|^{p} + ... + w_{n} \cdot |x_{in}-x_{jn}|^{p})^\frac{1}{p}$

通常 $\sum{i=1}^{n}w{i}=1$ 。

算法流程

给定样本集 $D = {x{1},x{2},…,x{m}}$ ，k均值聚类算法针对聚类所得簇划分 $C = {C{1},C{2},…,C{k}}$ 最小化平方误差

$min\ E = \sum_{i=1}^{k}\sum_{x \in C_{i}}\|x-\mu_{i}\|_{2}^{2}$

其中

$\mu_{i}=\frac{1}{|C_{i}|}\sum_{x \in C_{i}}x$

直接求解该式为NP hard问题，因此采用启发式迭代。

缺点

不能保证定位到聚类中心的最佳方案，但能保证收敛到某个具体方案，即局部最优点
算法无法指出类别数，在同一数据集中，选择不同类别得到的结果不同，甚至不合理

改进

多次聚类，初始化聚类中心不同，选择方差最小的结果
将类别设置为1,逐步提高类别数，一般情况下，总方差快速下降直到达到某个拐点，这意味着再加一个新的聚类中心也不会显著减少总体方差。

TODO…

python实现

参考资料

机器学习西瓜书

k均值聚类的理解和实现

K-Means聚类算法

杨安

正在开发中。。。

GitHub E-mail